Modelon製空調ライブラリと蒸気サイクルライブラリを使用したA/Cモデルシミュレーション速度の加速
This blog provides an introduction of the Spline-Based Table Look-up (SBTL) method as well as a sample use case from Ford Motor Company – who utilized the SBTL refrigerant package to speed up their air conditioning system model simulations.
SBTL is a modeling method used for processing large simulations in less time without compromising accuracy. As part of Modelon’s 2018.2 release of the Air Conditioning Library (ACL) and upcoming 2019.1 release of the Vapor Cycle Library (VCL), the SBTL method is integrated in each library to create new computationally efficient implementations of existing working fluids. This approach improves the tradeoff for air conditioning system model simplifications using ACL or VCL.
How SBTL works
The SBTL modeling method uses piece-wise quadratic splines on an equidistant grid to approximate refrigerant properties (denoted by ![]() ). The table lookup part of SBTL stems from the fact that using an equidistant grid enables a simple algorithm to retrieve spline coefficients from pre-generated tables, as shown in below equations where
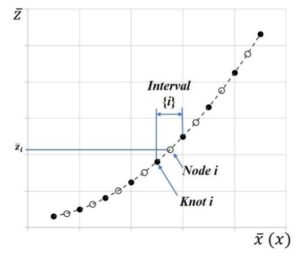
). The table lookup part of SBTL stems from the fact that using an equidistant grid enables a simple algorithm to retrieve spline coefficients from pre-generated tables, as shown in below equations where ![]() is the first knot. In Figure 1, nodes represent raw data points and knots are points where two adjacent splines meet with a continuous first-order derivative constraint.
is the first knot. In Figure 1, nodes represent raw data points and knots are points where two adjacent splines meet with a continuous first-order derivative constraint.
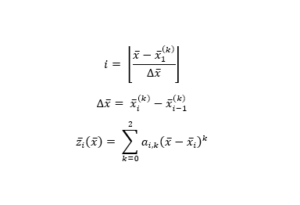
SBTL Implementation in ACL and VCL
Modelon has implemented R1234yf and R134a refrigerants using SBTL. The mediums are accessed from ACL and VCL in the exact same way as other two-phase medium implementations (e.g. drop-down list in Dymola). In order to reduce calculation time, C is used to implement evaluation, inversion, and differentiation of the quadratic splines. The used spline coefficients are derived a priori and afterward accessed from external data tables. However, the external C function calls do not impact the user-friendliness as the top level two-phase medium functions are all implemented in the Modelica language, thus wrapping the C functions and enabling easy access in simulation models. Figure 2 shows the implementation of the SBTL method in ACL and VCL.
Upon customer request, we can now add new SBTL media for any pure fluid that is available in REFPROP in a short amount of time. It is faster to add a new medium using the SBTL implementation than the equivalent Helmholtz model.

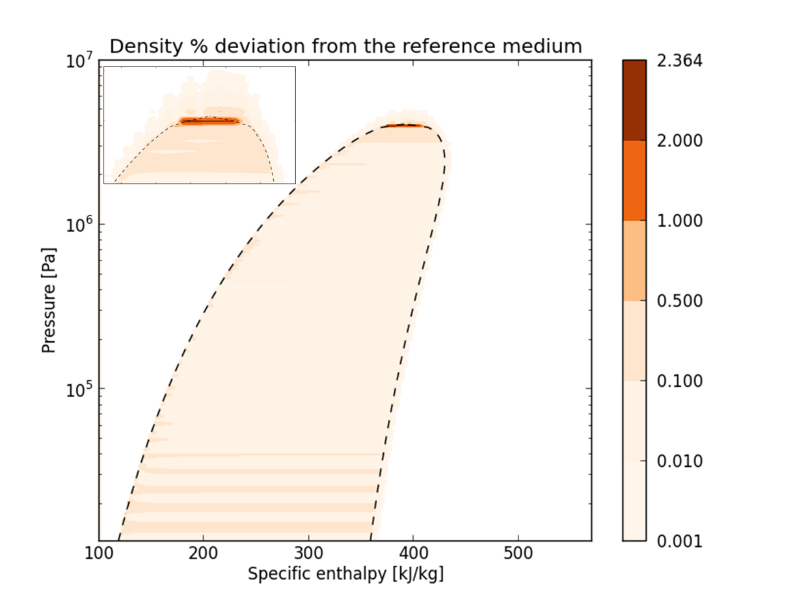
In Figure 3, the high accuracy of SBTL is exemplified for the R134a refrigerant with respect to density calculations. The comparison is done with the solution to the original Helmholtz equation. The only case when the error is larger than 2 % is inside the two-phase region, close to the critical point. Outside of this region, the error is well below 0.5 %.
Meanwhile, a substantial improvement in computation time is obtained with SBTL while maintaining high accuracy, as indicated by the results in Table 1.

Table 1 – Comparison of individual function calls between Helmhotz and SBTL implementations.
Application
Ford Motor Company worked with Modelon to try the new SBTL refrigerant package in efforts to speed up the AC system model simulations (read the full paper here). It is common to use the SC03 Supplemental Federal Test Procedure to represent emissions and engine load associated with air-conditioning systems in FTP-75 cycle certified vehicles. The system simulation model is described in Figure 4. The 1st evaporator, 2nd evaporator, and chiller are modeled using both SBTL and Helmholtz based implementations of R1234yf for simulation performance comparison.
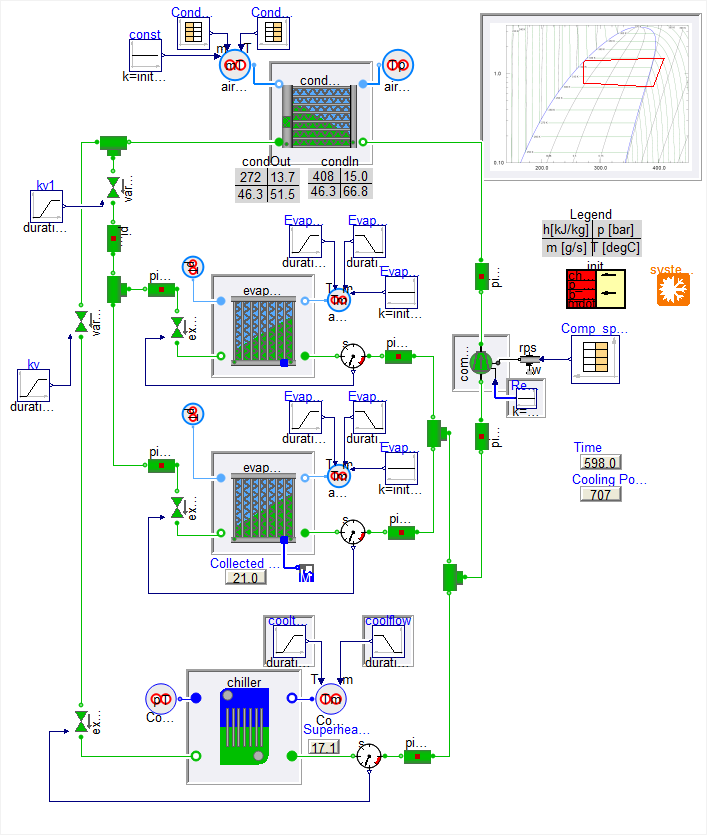
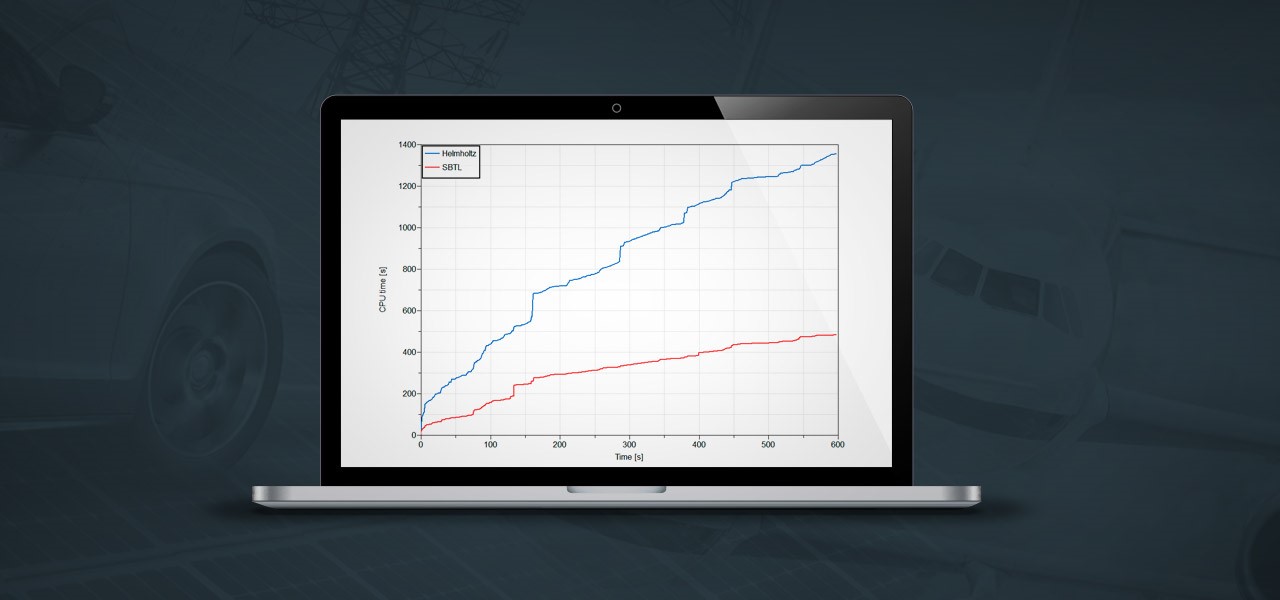
The calculation performance for the different subsystems is compared with respect to R1234yf implementation in Figs 5-6. It can be concluded that using the SBTL refrigerant model it is possible to simulate the complete SC03 cycle faster than the real total cycle time (598 s) while keeping the same numerical performance as the Helmholtz based model.
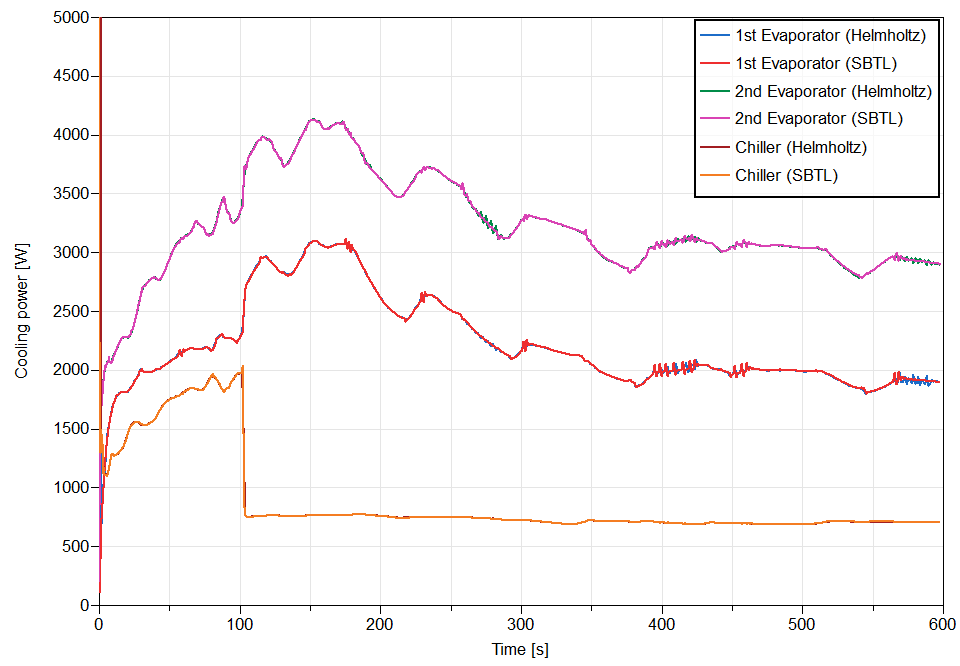
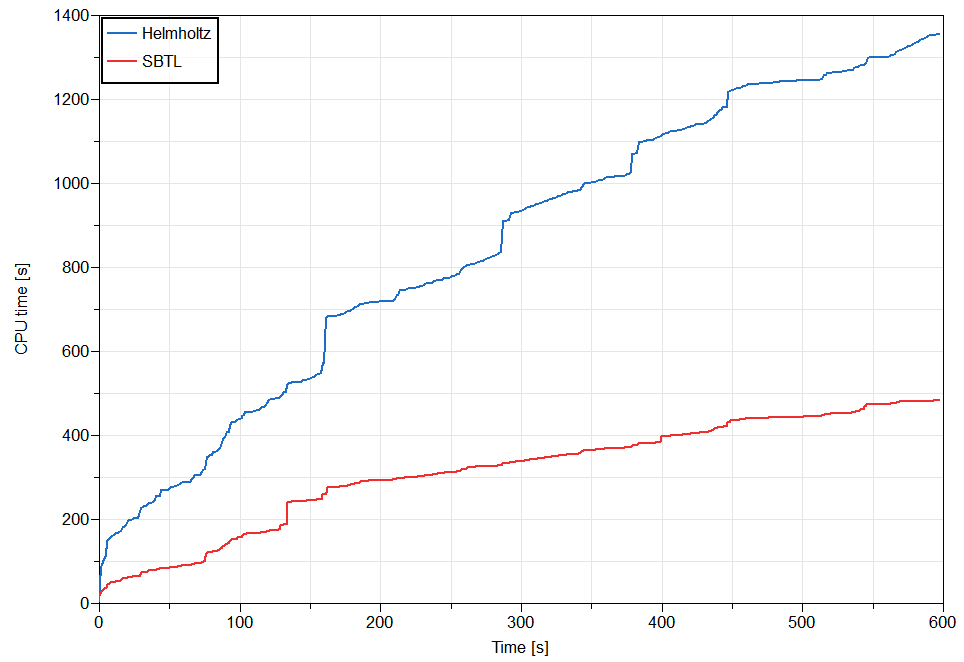
More in-depth information on what SBTL refrigerants in ACL and VCL has to offer can be found in [1]. If you are curious what Modelon can contribute to your business when it comes to accurate and fast system model simulations, contact us below.
[1]: “Fast Calculation of Refrigerant Properties in Vapor Compression Cycles Using Spline-Based Table Look-Up Method (SBTL)”, Lixiang Li et al., Proceedings of the 1st American Modelica Conference, 2018, https://doi.org/10.3384/ecp1815477.


